非同調性隨機雷射的蒙地卡羅模擬計算
劉建軒、高宗聖
一般雷射輸出需設計及製備良好的共振腔結構。而每個共振腔根據其設計及尺寸之不同會支持不同的共振頻率,這些特定共振頻率即被稱為模態(mode)。然而,在隨機雷射(random laser)中,光波的回饋機制則由系統中隨機散佈的散射體甚或是缺陷所提供的。因此,隨機雷射的模態在空間和光譜行為表現上都被認為是隨機產生的。隨機雷射作用可以在許多材料中觀察,例如,微米尺寸的鈣鈦礦晶體(microcrystalline perovskites)1,2、生物組織3、摻有奈米顆粒的染料介質(dye materialss)4、半導體粉末5等等。從觀察隨機雷射其輻射光譜特徵,可分為非同調性(incoherent)隨機雷射及同調性(coherent)隨機雷射6。
非同調性的隨機雷射放光通常被認為是非共振式回饋(non-resonant feedback)或稱為強度回饋(intensity feedback)機制,是基於在增益介質中的光子擴散(photon diffusion)。當輸入能量密度達到閾值時,隨機雷射輻射光譜中可觀察到數個奈米寬度的輻射尖峰產生。由於光子的擴散,所以強度的空間輪廓在系統中是延伸的。另一方面,同調性隨機雷射則被認為是共振回饋(resonant feedback)或是場回饋(field feedback)機制主導。與傳統雷射相似,即需要滿足相位條件。在這種類型的雷射作用中,在光譜中可發現約為0.2~0.5奈米線寬的輻射尖峰,並可預期在某些區域出現強度的空間限制。
光子擴散對於理解非同調性隨機發光是非常重要的7。因此,我們利用蒙地卡羅方法(Monte Carlo method)來模擬光子在無序增益介質中的擴散情況。在過程中,我們根據米氏理論(Mie theory)對每個光子施加隨機路徑(random walk)條件,配合依實驗量測而得的吸收和發射截面(absorption and emission cross section),我們可以進一步追蹤光子在擴散出系統之前的總放大量。圖1(a)展示了在Ph6G染料介質中有無摻雜二氧化鈦(TiO2)散射體(直徑約為410奈米),在不同作用能量密度下,其光譜峰值線寬的模擬結果比較。模擬結果清楚地表明光子散射是產生隨機雷射作用的重要關鍵之一。為了再進一步地瞭解光子散射在隨機雷射作用產生的重要性,圖1(b)顯示了平均自由路徑(mean free path)為1.5和3微米時,入射光作用面積(pumping area)與雷射閾值間的相依關係,可發現閾值與激發面積和散射平均自由路徑高度相關,這是在無序的增益介質中光子擴散的結果。
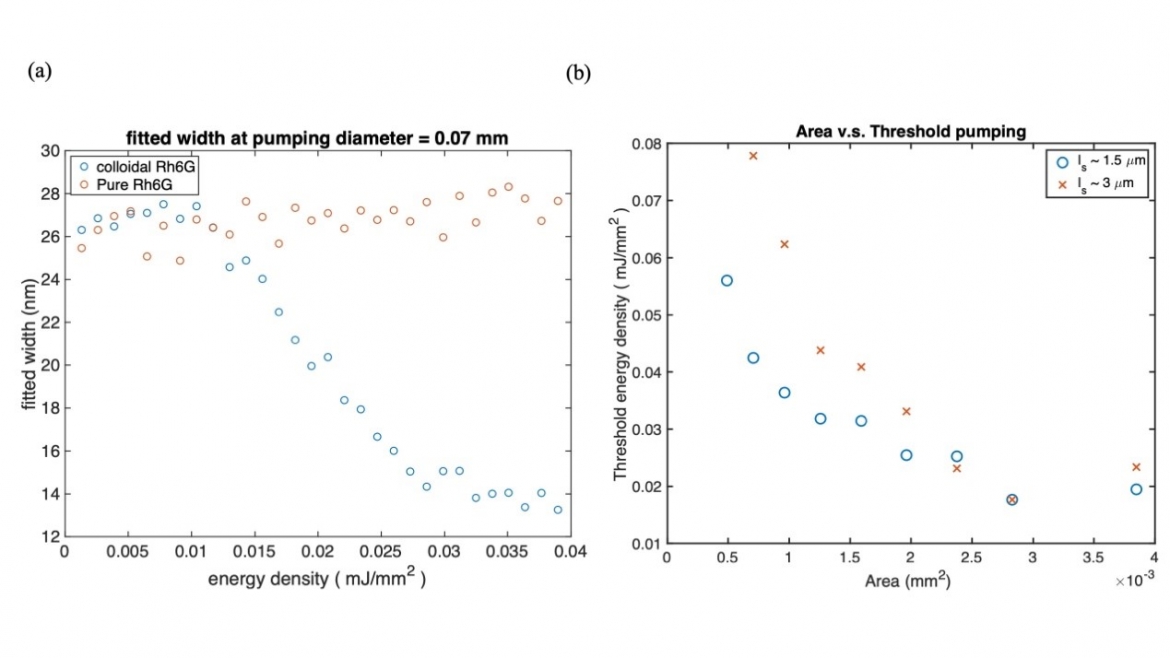
Fig. 1 (a) Simulated linewidth of colloidal Rh6G and pure Rh6G (pumping diameter D =0.7 mm) (b) Area-Threshold curve with two scattering mean free path (ls represents scattering mean-free path)
此外,我們也模擬散射體其米氏共振(Mie resonance)對發射光譜的影響。在圖2中,我們在染料介質中摻雜直徑為900奈米的TiO2散射體,並計算其傳輸平均自由路徑光譜(transport mean free path),即各向異性散射(anisotropic scattering)的散射平均自由路徑的修正版項。沿著傳輸平均自由路徑光譜,可發現輻射峰值出現在約563奈米和571奈米處,其間分別發生了最大增益和米氏共振結果。此外,兩個輻射尖峰的線寬與米氏共振線寬一致,即說明米氏共振影響發射光譜的有力證據。
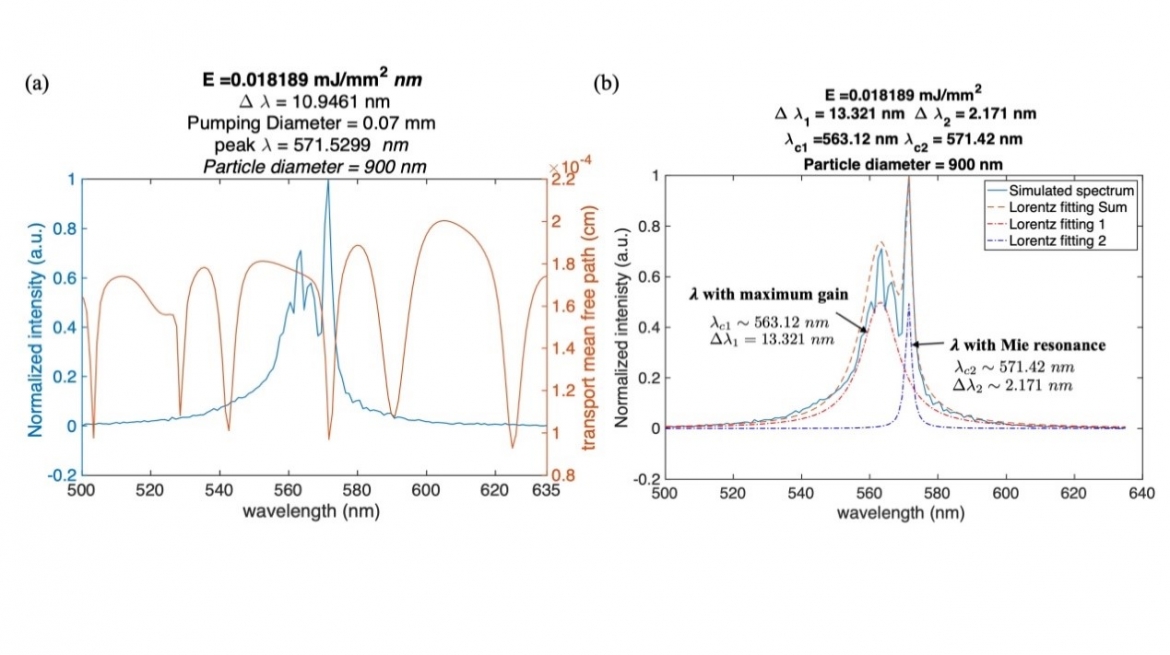
Fig. 2 (a) Simulated emission spectrum with TiO2 scatterings with 900 nm in diameter, along with its transport mean free path spectrum (b) A further curve fitting with respect to two peaks at 563.12 nm and 571.42 nm.
參考文獻
1. R. Dhanker, A. N. Brigeman, A. V. Larsen, R. J. Stewart, J. B. Asbury, and N. C. Giebink, “Random lasing in organo-lead halide perovskite microcrystal networks”, Appl. Phys. Lett., 105 151112, (2014)
2. Y. C. Wang, H. Li, Y. -H. Hong, K. -B. Hong, F. -C. Chen, C. -H. Hsu, R. -K. Lee, C. Conti, T. S. Kao, and T. -C. Lu, “Flexible organometal−halide perovskite lasers for speckle reduction in imaging projection”, ACS Nano, 13 5424, (2019)
3. R. C. Polson and Z. V. Vardeny, “Random lasing in human tissues”, Appl. Phys. Lett., 85 1289, (2004)
4. N. M. Lawandy, R. M. Balachandran, A. S. L. Gomes, and E. Sauvain, “Laser action in strongly scattering media”, Nature, 368 436, (1994)
5. H. Cao, Y. G. Zhao, S. T. Ho, E. W. Seelig, Q. H. Wang, and R. P. H. Chang, “Random laser action of semiconductor powder”, Phys. Rev. Lett., 82 2278, (1999)
6. F. Luan et al., “Lasing in nanocomposite random media,” Nano Today, 10 168., (2015)
7. V. S. Letokhov, “Generation of light by a scattering medium with negative resonance absorption”, Soviet Phys. JETP, 26 835, (1968)
BACK
